中缀表达式

人类正常使用的表达式，如：

例子

• 1 + 2 * 3- 5
• 2 * ( 14 + 2 ) - 33
  若不用括号，那么中缀表达式可能会有歧义

后缀表达式

逆波兰表示法（Reverse Polish notation，RPN，或逆波兰记法），是一种是由波兰数学家扬·武卡谢维奇1920年引入的数学表达式方式，在逆波兰记法中，所有操作符置于操作数的后面，因此也被称为后缀表示法。逆波兰记法不需要括号来标识操作符的优先级。

解释

逆波兰记法中，操作符置于操作数的后面。例如表达“三加四”时，写作“3 4 +”，而不是“3 + 4”。如果有多个操作符，操作符置于第二个操作数的后面，所以常规中缀记法的“3 - 4 + 5”在逆波兰记法中写作“3 4 - 5 +”：先3减去4，再加上5。使用逆波兰记法的一个好处是不需要使用括号。例如中缀记法中“3 - 4 5”与“（3 - 4）5”不相同，但后缀记法中前者写做“3 4 5 -”，无歧义地表示“3 (4 5 ) −”；后者写做“3 4 - 5 *”。

逆波兰表达式的解释器一般是基于堆栈的。解释过程一般是：操作数入栈；遇到操作符时，操作数出栈，求值，将结果入栈；当一遍后，栈顶就是表达式的值。因此逆波兰表达式的求值使用堆栈结构很容易实现，并且能很快求值。

注意：逆波兰记法并不是简单的波兰表达式的反转。因为对于不满足交换律的操作符，它的操作数写法仍然是常规顺序，如，波兰记法“/ 6 3”的逆波兰记法是“6 3 /”而不是“3 6 /”；数字的数位写法也是常规顺序。

例子

同中缀表达式例子

• 1 2 3 * + 5 -
• 14 2 + 2 * 33 -

前缀表达式

波兰表示法（Polish notation，或波兰记法），是一种逻辑、算术和代数表示方法，其特点是操作符置于操作数的前面，因此也称做前缀表示法。如果操作符的元数（arity）是固定的，则语法上不需要括号仍然能被无歧义地解析。波兰记法是波兰数学家扬·武卡谢维奇1920年代引入的，用于简化命题逻辑。
扬·武卡谢维奇本人提到

我在1924年突然有了一个无需括号的表达方法，我在文章第一次使用了这种表示法。 ”
—— Łukasiewicz(1), p. 610, footnote.

例子

同中缀表达式例子

• - + 1 * 2 3 5
• - * + 14 2 2 33

树的解释

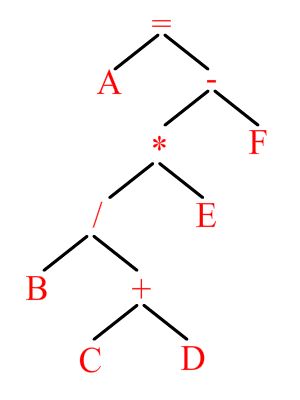
中序遍历结果为：A=B/ C+DE-F对应着 中缀表达式 为：A=B/ C+DE-F
前序遍历结果为：=A-/B+CDEF对应着 前缀表达式 为：=A-/B+CDEF
后序遍历结果为：ABCD+/EF-=对应着 后缀表达式 为：ABCD+/EF-=