描述
用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。Dijkstra算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率低。
Dijkstra算法
描述
Dijkstra算法(迪杰斯特拉)是典型的最短路径路由算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。Dijkstra算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率低。可以用堆优化。
其采用的是贪心法的算法策略
大概过程:
创建两个表,OPEN, CLOSE。
OPEN表保存所有已生成而未考察的节点,CLOSED表中记录已访问过的节点。
1. 访问路网中距离起始点最近且没有被检查过的点,把这个点放入OPEN组中等待检查。
2. 从OPEN表中找出距起始点最近的点,找出这个点的所有子节点,把这个点放到CLOSE表中。
3. 遍历考察这个点的子节点。求出这些子节点距起始点的距离值,放子节点到OPEN表中。
4. 重复第2和第3步,直到OPEN表为空,或找到目标点。
C/C++代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72
| #include <stdio.h> #include <iostream> #include <algorithm> #include <math.h> #include <cstring> using namespace std; #define inf 0xffff; int mp[11][11],dis[11],pre[11]; bool isvitied[11]; int n,m,s; void init(){ memset(pre,0,sizeof(pre)); memset(isvitied,0,sizeof(isvitied)); printf(" 请输入点数和边数"); cin>>n>>m; printf("请输入起点"); cin>>s; for(int i=0;i<=10;i++) for(int j=0;j<=10;j++) mp[i][j]=inf; for(int i=0;i<=10;i++) mp[i][i]=0; for(int i=0;i<=10;i++) dis[i]=inf; dis[s]=0; printf("请输入边的端点和权值"); for(int i=1;i<=m;i++) { int a,b,c; cin>>a>>b>>c; mp[a][b]=c; mp[b][a]=c; } } int last; int dijkstra(){ int ans=0; for(int i=1;i<=n;i++){ int u=0; for(int j=1;j<=n;j++) if(!isvitied[j]&&dis[j]<dis[u]) u=j; ans+=dis[u]; last=u; isvitied[u]=1; for(int j=1;j<=n;j++) if(!isvitied[j]&&mp[u][j]+dis[u]<dis[j]){ dis[j]=mp[u][j]+dis[u]; pre[j]=u; } } return ans; } void dp(int x){ if(x!=0) { dp(pre[x]); printf("%d ",pre[x]); } } int main() { init(); int e=dijkstra(); printf("请输入终点\n"); cin>>e; printf("最短路是 %d \n",dis[e]); return 0; }
|
输入
6 10
1
1 3 1
1 4 5
1 2 6
2 3 5
2 5 3
3 4 5
3 6 4
3 5 6
4 6 2
5 6 6
5
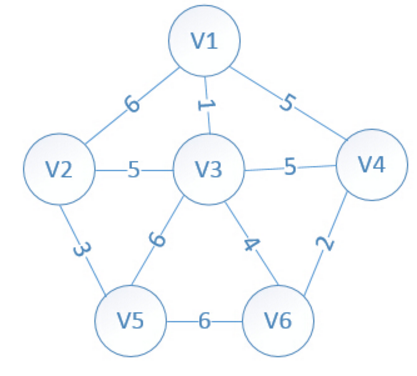
输出
以1为起点的,5为终点的最短路径的权值之和。
心得
Prim算法和Dijkstra算法本质是一样的,都是贪心。他们的算法代码也几乎一致。
