描述
一个有n个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有n个结点,并且有保持图连通的最少的边。 最小生成树可以用kruskal(克鲁斯卡尔)算法或prim(普里姆)算法求出。
Prim算法
描述
Prim算法简述
1). 输入:一个加权连通图,其中顶点集合为V,边集合为E;
2). 初始化:Vnew= {x},其中x为集合V中的任一节点(起始点),Enew= {},为空;
3). 重复下列操作,直到Vnew= V:
a.在集合E中选取权值最小的边,其中u为集合Vnew中的元素,而v不在Vnew集合当中,并且v∈V(如果存在有多条满足前述条件即具有相同权值的边,则可任意选取其中之一);
b.将v加入集合Vnew中,将边加入集合Enew中;
4). 输出:使用集合Vnew和Enew来描述所得到的最小生成树。[1]
C/C++代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62
| #include <stdio.h> #include <iostream> #include <algorithm> #include <math.h> #include <cstring> using namespace std; #define inf 0xffff; int mp[11][11],dis[11],pre[11]; bool isvitied[11]; int n,m,s; void init(){ memset(pre,0,sizeof(pre)); memset(isvitied,0,sizeof(isvitied)); printf("请输入点数和边数"); cin>>n>>m; printf("请输入起点"); cin>>s; for(int i=0;i<=10;i++) for(int j=0;j<=10;j++) mp[i][j]=inf; for(int i=0;i<=10;i++) mp[i][i]=0; for(int i=0;i<=10;i++) dis[i]=inf; dis[s]=0; printf("请输入边的端点和权值"); for(int i=1;i<=m;i++) { int a,b,c; cin>>a>>b>>c; mp[a][b]=c; mp[b][a]=c; } } int last; int prime(){ int ans=0; for(int i=1;i<=n;i++){ int u=0; for(int j=1;j<=n;j++) if(!isvitied[j]&&dis[j]<dis[u]) u=j; ans+=dis[u]; last=u; isvitied[u]=1; for(int j=1;j<=n;j++) if(!isvitied[j]&&mp[u][j]<dis[j]){ dis[j]=mp[u][j]; pre[j]=u; } } return ans; } int main() { init(); printf("生成树权值之和 %d \n",prime()); return 0; }
|
输入
6 10
1
1 3 1
1 4 5
1 2 6
2 3 5
2 5 3
3 4 5
3 6 4
3 5 6
4 6 2
5 6 6
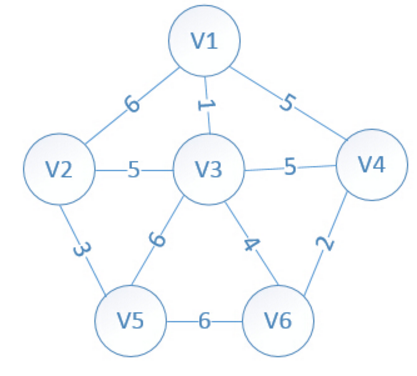
输出
以1为起点的最小生成树的权值之和。
