描述

凸包是什么?直接上图……
凸包

摸板基础

平面几何关于点的模板
平面几何

求解凸包

凸包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//求凸包
vector <P>  convex_hull(P * ps,int n){
   sort(ps ,ps +n  , cmp_x);
   int k = 0 ;//凸包的顶点个数
   vector<P> qs (2*n);
   for(int i= 0 ; i< n ; i++ ){
        while( k > 1 && (qs[k-1] - qs[k-2]).det(ps[i]-qs[k-1]) <= 0)k--;
        qs[k++] = ps[i];
   }
   for(int i = n - 2 , t = k ; i >= 0 ; i--){
        while( k > t && (qs[k-1] - qs[k-2]).det(ps[i]-qs[k-1]) <= 0)k--;
        qs[k++] = ps[i];
   }
   qs.resize(k-1);
   return qs;
}

求凸包中的最远点距

暴力扫

复杂度O(n*n)

1
2
3
4
5
6
7
8
9
10
double solve_1(){
    vector <P> qs = convex_hull(ps,n);
    double res=0;
    for(int i = 0 ; i <qs.size() ; i++){
        for(int j = 0 ; j< i ; j ++){
            res=max(res,dist(qs[i] , qs[j]));
        }
    }
    return res;
}

旋转卡壳法

复杂度O(n)
旋转卡壳法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
double Rotatingcalipers(){
    vector <P> qs = convex_hull(ps,n);
    int num = qs.size();
    if( num == 2){//处理凸包退化的情况
        printf("%.0f\n",dist(qs[0] ,qs[1]));
        return ; 
    }
    int i = 0 , j = 0;//某个方向上的对踵点对
    for(int k = 0 ; k < num ; k++){
        if(!cmp_x(qs[i] , qs[k])) i = k ;
        if( cmp_x(qs[j] , qs[k])) j = k ;
    }
    double res = 0;
    int si = i , sj = j ;
    while(i != sj || j != si){
        res = max(res , dist(qs[i] , qs[j]));
        if((qs[(i+1) % num] - qs[i]).det(qs[(j+1)%num] - qs[j]) < 0){
            i = ( i + 1 ) % num ;
        }else{
            j = ( j + 1) % num;
        }
    }
    return res;
}

POJ_2187

题意

一堆点，求出一个凸包，求凸包的最远点对距离

AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
#include <iostream>
#include <cmath>
#include <cstring>
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
const double eps=1e-10;
#define NV 50005
//考虑就误差的加法
int n;
double add(double a , double b){
    if(fabs(a+b) < eps * ( fabs(a)+fabs(b) ) ) return 0;
    return a + b;
}
struct P{
    double x,y;
    P (){ }
    P (double a, double b):x(a),y(b){}
    P operator + (P p){
        return P( add(x , p.x) , add(y , p.y));
    }
    P operator - (P p){
        return P( add(x, -p.x) , add( y ,-p.y));
    }
    P operator * (double d){
        return P( x * d , y * d);
    }
    double dot (P p){//内积
        return add( x * p.x , y * p.y);
    }
    double det (P p){//外积
        return add( x * p.y , -y * p.x);
    }
};
bool on_seg(P p1,P p2 ,P q){//判断q点是否在线段(p1-p2)上 
    return (p1 - q).det(p2 - q)==0 && (p1 -q).dot(p2 - q) <= 0;
}
P intersection(P p1, P p2 ,P q1 , P q2){//计算直线(p1-p2)与(q1-q2)的
    return p1 +  (p2 - p1)*((q2 - q1).det(q1 - p1) / (q2 - q1).det(p2 - p1));
}
bool parallel(P p1 , P p2 , P q1 , P q2){//判断(p1-p2)和(q1-q2)是否平行，平行返回1
    return (p1-p2).det(q1-q2)==0? 1 : 0 ;
}
P ps[NV];
//字典序比较
bool cmp_x(const P &p , const P &q){
    if(p.x!=q.x)return p.x < q.x;
    return p.y < q.y;
}
double dist(P p, P q){
    return (p-q).dot(p-q);
}
//求凸包
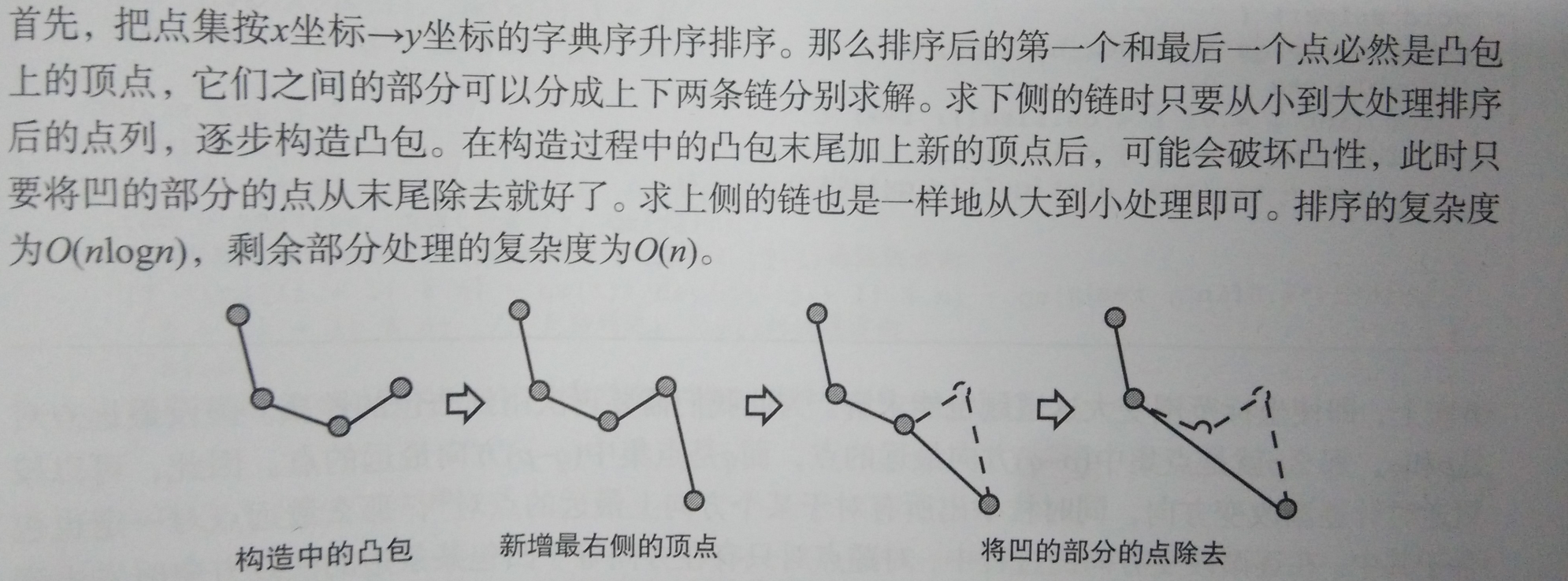
vector <P>  convex_hull(P * ps,int n){
   sort(ps ,ps +n  , cmp_x);
   int k = 0 ;//凸包的顶点个数
   vector<P> qs (2*n);
   for(int i= 0 ; i< n ; i++ ){
        while( k > 1 && (qs[k-1] - qs[k-2]).det(ps[i]-qs[k-1]) <= 0)k--;
        qs[k++] = ps[i];
   }
   for(int i = n - 2 , t = k ; i >= 0 ; i--){
        while( k > t && (qs[k-1] - qs[k-2]).det(ps[i]-qs[k-1]) <= 0)k--;
        qs[k++] = ps[i];
   }
   qs.resize(k-1);
   return qs;
}
void solve_1(){
    vector <P> qs = convex_hull(ps,n);
    double res=0;
    for(int i = 0 ; i <qs.size() ; i++){
        for(int j = 0 ; j< i ; j ++){
            res=max(res,dist(qs[i] , qs[j]));
        }
    }
    printf("%.0f\n",res);
}
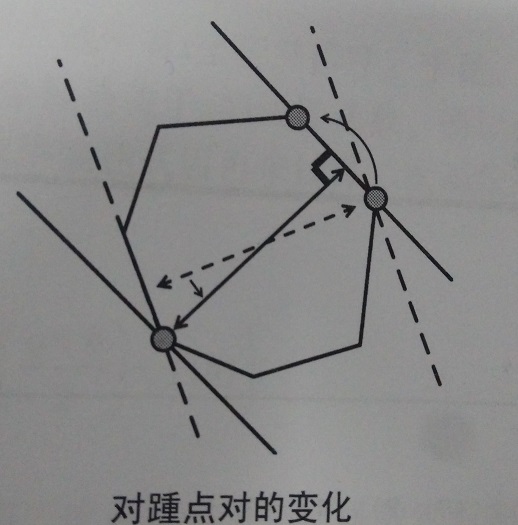
void Rotatingcalipers(){
    vector <P> qs = convex_hull(ps,n);
    int num = qs.size();
    if( num == 2){//处理凸包退化的情况
        printf("%.0f\n",dist(qs[0] ,qs[1]));
        return ; 
    }
    int i = 0 , j = 0;//某个方向上的对踵点对
    for(int k = 0 ; k < num ; k++){
        if(!cmp_x(qs[i] , qs[k])) i = k ;
        if( cmp_x(qs[j] , qs[k])) j = k ;
    }
    double res = 0;
    int si = i , sj = j ;
    while(i != sj || j != si){
        res = max(res , dist(qs[i] , qs[j]));
        if((qs[(i+1) % num] - qs[i]).det(qs[(j+1)%num] - qs[j]) < 0){
            i = ( i + 1 ) % num ;
        }else{
            j = ( j + 1) % num;
        }
    }
    printf("%.0lf\n",res);
}
void init(){
    scanf("%d",&n);
    for(int i=0 ; i <  n ; i++ )scanf("%lf%lf",&ps[i].x,&ps[i].y);
}
int main()
{   
    init();
    //solve_1();
    Rotatingcalipers();
    return 0;
}