描述

本福特定律，也称为本福特法則，说明一堆从实际生活得出的数据中，以1为首位数字的数的出现概率约为总数的三成，接近期望值1/9的3倍。推广来说，越大的数，以它为首几位的数出现的概率就越低。它可用于检查各种数据是否有造假。

解释

本福特定律说明在 {\displaystyle b} b进位制中，以数 n起头的数出现的概率为 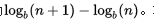。本福特定律不但适用于个位数字，连多位的数也可用。
在十进制首位数字的出现概率（%，小数点后一个位）：

数 概率
1 30.1%
2 17.6%
3 12.5%
4 9.7%
5 7.9%
6 6.7%
7 5.8%
8 5.1%
9 4.6%

HDU_5051

题意

给定n，b，q。对于无限长数列的a[]，ai = b*q^i。问n是ai的前缀的概率。

AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <cstdio>
#include <map>
using namespace std;
#define ll long long
#define mod 2147483647
#define inf 0x3f3f3f3f 
int main()  
{  
  int T,ca=0;  
  for(cin>>T;T--;){
    int n,b,q;  
    scanf("%d%d%d",&n,&b,&q);  
    double ans;
    if (q==10||q==100||q==1000){ 
            if (b==n||b/10==n||b/100==n||b/1000==n||b*10==n||b*100==n||b*1000==n) ans=1;  
            else ans=0;
    }
    else{  
        if (q==1){
            if (b==n||b/10==n||b/100==n||b/1000==n) ans=1;  
            else ans=0;  
          }
        else ans=log10((double)(n+1)/double(n));   
    }
    printf("Case #%d: %.5f\n",++ca,ans);  
  }  
  return 0;  
}