树链剖分王氏解释
当你有一棵树,你要修改A点到B点路径上的点权或者边权时,傻傻地就会LCA然后巴拉巴拉找爸爸,顺便修改点权和边权,其实有了树链剖分就不用这样。
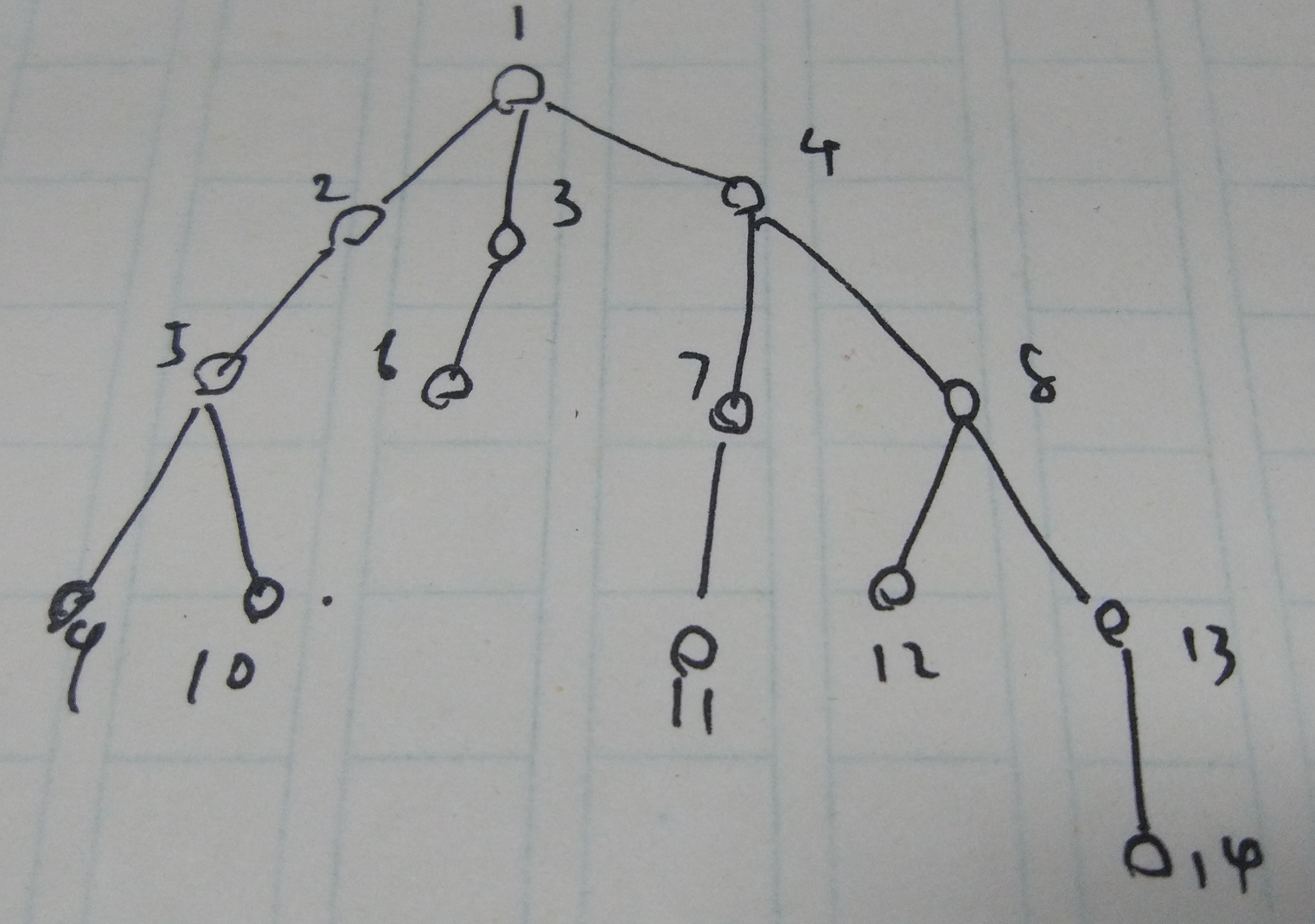
你有一颗树,每次从中抽出一条尽量长的一条枝,然后用线段树或其他数据结构去维护它不就行了?

这就是树链剖分的本意。
大神解释
starszys的博客
使用方法
work(n)初始化,注意输入点权和输入树的先后关系,默认点下标从1开始,树根为1
find(x,y) 求x,y路径上的点权和(或最值,可通过修改线段树得到)
update(w[x],y,1,n) 将x节点的权值更新为y
因为有dfs和建树函数,在数据量大的时候会爆栈,所以手动扩展
1 2
| #pragma comment(linker, "/STACK:10240000000,10240000000")
|
模板
by门一凡网站的邹卓君模板
点权型 单点更新 区间查询
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112
| #define lson l,m,rt<<1 #define rson m+1,r,rt<<1|1 const int Vmax = 5*1e4 + 5; const int Emax =2*1e5+5; namespace segment_tree{ int sum[Vmax<<2],add[Vmax<<2]; inline void pushup(int rt){ sum[rt]=sum[rt<<1]+sum[rt<<1|1]; } void update(int L,int c,int l,int r,int rt=1){ if (L == l && l == r) { sum[rt] = c; return ; } int m = (l + r) >> 1; if (L <= m) update(L , c , lson); else update(L , c , rson); pushup(rt); } int query(int L,int R,int l,int r,int rt=1){ if (L <= l && r <= R) return sum[rt]; int m = (l + r) >> 1; int ret = 0; if (L <= m) ret+=query(L , R , lson); if (m < R) ret+=query(L , R , rson); return ret; } } namespace poufen{ using namespace segment_tree; int siz[Vmax],son[Vmax],fa[Vmax],dep[Vmax],top[Vmax],w[Vmax]; int nodenum; struct edge{ int v,next; }e[Emax]; int pre[Vmax],ecnt; inline void init(){ memset(pre, -1, sizeof(pre)); ecnt=0; } inline void add_(int u,int v){ e[ecnt].v=v; e[ecnt].next=pre[u]; pre[u]=ecnt++; } void dfs(int u){ siz[u]=1;son[u]=0; for(int i=pre[u];~i;i=e[i].next) { int v=e[i].v; if(fa[u]!=v) { fa[v]=u; dep[v]=dep[u]+1; dfs(v); siz[u]+=siz[v]; if(siz[v]>siz[son[u]])son[u]=v; } } } void build_tree(int u,int tp){ top[u]=tp,w[u]=++nodenum; if(son[u])build_tree(son[u],tp); for(int i=pre[u];~i;i=e[i].next) if(e[i].v!=fa[u]&&e[i].v!=son[u]) build_tree(e[i].v,e[i].v); } inline int find_point(int u,int v){ int ret=0; int f1=top[u],f2=top[v]; while(f1!=f2) { if(dep[f1]<dep[f2]) swap(f1,f2),swap(u,v); ret+=query(w[f1],w[u],1,nodenum); u=fa[f1]; f1=top[u]; } if(dep[u]>dep[v])swap(u,v); ret+=query(w[u],w[v],1,nodenum); return ret; } int a[Vmax],b[Vmax]; int val[Vmax]; void work_point(int n) { memset(siz, 0, sizeof(siz)); memset(sum, 0, sizeof(sum)); init(); int root=1; fa[root]=nodenum=dep[root]=0; for(int i=1;i<=n;i++) scanf("%d",&val[i]); for(int i=1;i<n;i++) { scanf("%d%d",&a[i],&b[i]); add_(a[i],b[i]); add_(b[i],a[i]); } dfs(root); build_tree(root,root); for(int i=1;i<=n;i++) update(w[i],val[i],1,nodenum); } } using namespace poufen;
|
边权型
替换不同的find函数和work函数
边权的组织原理就是在确认树根后,边权向下对应,就是a点记录a点到a的爸爸的边的权值。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42
| inline int find_egde(int u,int v){ int f1=top[u],f2=top[v],ret=0; while(f1!=f2) { if(dep[f1]<dep[f2]) swap(f1,f2),swap(u,v); ret+=query(w[f1],w[u],1,nodenum); u=fa[f1]; f1=top[u]; } if(u==v)return ret; if(dep[u]>dep[v])swap(u,v); return ret+=query(w[son[u]],w[v],1,nodenum); } void work_edge(int n){ memset(siz, 0, sizeof(siz)); memset(sum, 0, sizeof(sum)); init(); int root=1; fa[root]=nodenum=dep[root]=0; for(int i=1;i<n;i++) { scanf("%d%d%d",&a[i],&b[i],&c[i]); add_(a[i],b[i]); add_(b[i],a[i]); } dfs(root); build_tree(root,root); for(int i=1;i<n;i++){ int u = a[i]; int v = b[i]; if (dep[u] > dep[v]) { //保证v是被指向的点,也就是深度较大的点 swap(u, v); swap(a[i], b[i]); } update(w[v],c[i],1,nodenum); } }
|
区间更新
u,v路径上的点或者边的权值更新
点
1 2 3 4 5 6 7 8 9 10 11 12 13
| inline void upd_point(int u,int v,int c){ int f1=top[u],f2=top[v] while(f1!=f2) { if(dep[f1]<dep[f2]) swap(f1,f2),swap(u,v) update(w[f1],w[u],c,1,nodenum) u=fa[f1] f1=top[u] } if(dep[u]>dep[v])swap(u,v) update(w[u],w[v],c,1,nodenum) }
|
边
1 2 3 4 5 6 7 8 9 10 11 12 13 14
| inline void upd_edge(int u,int v,int c){ int f1=top[u],f2=top[v] while(f1!=f2) { if(dep[f1]<dep[f2]) swap(f1,f2),swap(u,v) update(w[f1],w[u],c,1,nodenum) u=fa[f1] f1=top[u] } if(u==v)return if(dep[u]>dep[v])swap(u,v) update(w[son[u]],w[v],c,1,nodenum) }
|

