工作环境
Windows10 SAS9.4
实验数据
150余条历史人民币和美元的汇率,和 的3.6上机指导。
的3.6上机指导。
实验步骤和原理
判断是否平稳
方法一
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
| data example3_1; input x@@; time=_n_; cards; 0.30 -0.45 0.36 0.00 0.17 0.45 2.15 4.42 3.48 2.99 1.74 2.4 0.11 0.96 0.21 -0.10 -1.27 -1.45 -1.19 -1.47 -1.34 -1.02 -0.27 0.14 -0.07 0.10 -0.15 -0.36 -0.50 -1.93 -1.49 -2.35 -2.18 -0.39 -0.52 -2.24 -3.46 -3.97 -4.60 -3.09 -2.19 -1.21 0.78 0.88 2.07 1.44 1.50 0.29 -0.36 -0.97 -0.30 -0.28 0.80 0.91 1.95 1.77 1.80 0.56 -0.11 0.10 -0.56 -1.34 -2.47 0.07 -0.69 -1.96 0.04 1.59 0.20 0.39 1.06 -0.39 -0.16 2.07 1.35 1.46 1.50 0.94 -0.08 -0.66 -0.21 -0.77 -0.52 0.05 ; proc gplot data=example3_1; plot x * time=1; symbol1 c=red I=join v=star; run;
|
可以根据时序图来判断该序列是否平稳,但是这种判断方式主观影响很大。
平稳序列:在一个定值附近来回波动,无周期,无明显趋势。
非平稳序列:有周期或者明显趋势。
方法二
1 2 3
| proc arima data = example3_1; identify Var=x nlag=8; run;
|
“nlag=8”的意义是规定运算8延迟阶数。在普通测试时不一定确定具体的阶数,可以先不写。
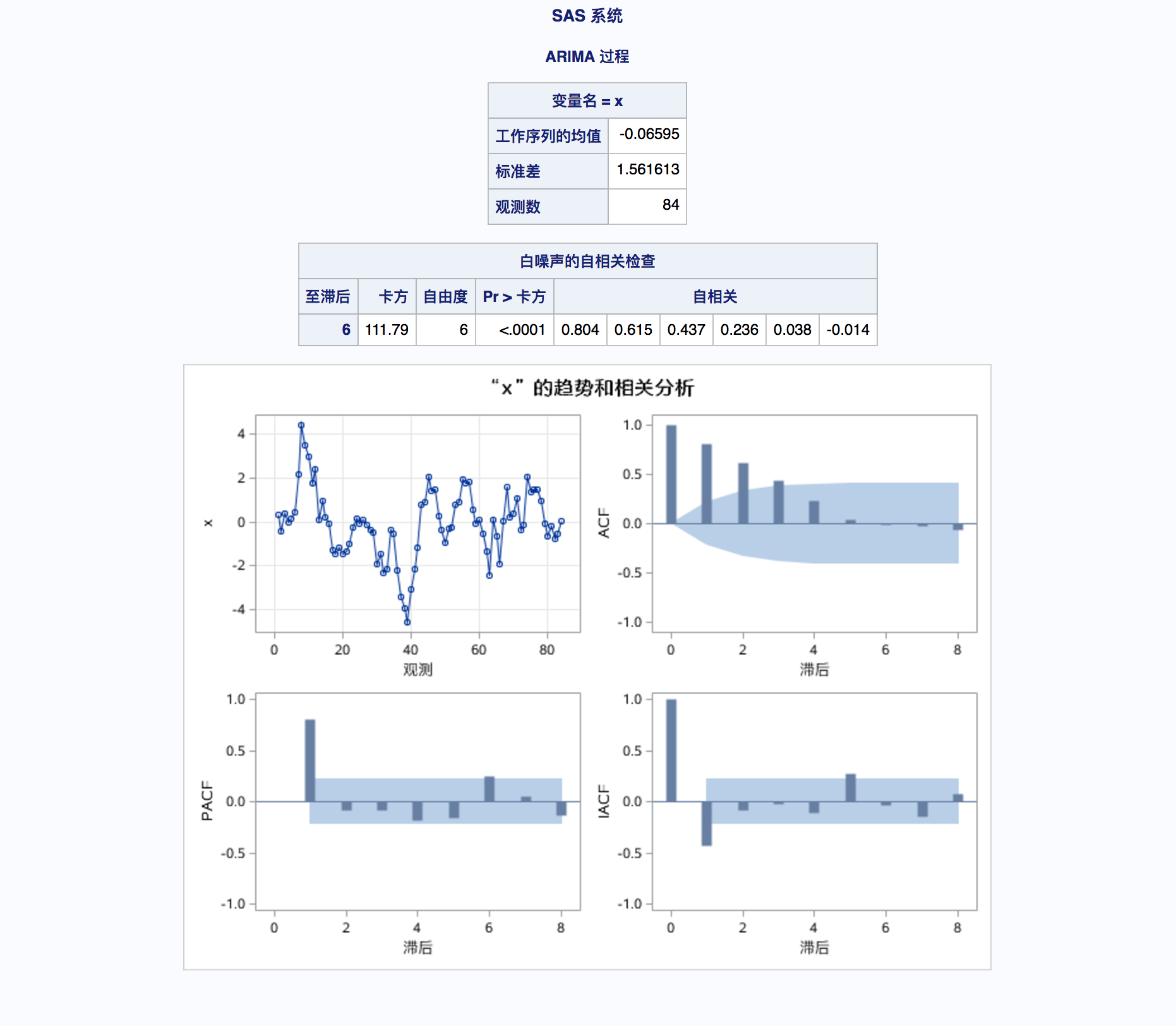
ACF:(即Autocorrelation Function)自相关图
PACF:(即Partial Autocorrelation Function)偏自相关图
IACF:(即Inverse Autocorrelation Function)逆自相关图
判断拖尾和截尾传送门。
截尾:ACF或者PACF在最初d阶明显超过2倍标准差范围,而后几乎95%ACF在2倍标准差的范围之内,ACF从非零衰减为小值波动过程非常突然。则是为d阶截尾
拖尾:超过5%ACF在2倍标准差的范围之外,ACF从非零衰减为小值波动过程比较缓慢或非常连续。则是不截尾,即拖尾。
平稳序列:1、系数很快落入两倍标准差范围内。(高台跳水,水花点点)
非平稳序列:1、自相关系数递减缓慢,图形对称三角形。2、有周期性。
白噪声检测
这部分还不是很懂,略……
判断最优模型
1 2 3
| proc arima data = example3_1; identify Var=x nlag=8 minic p=(0:5)q=(0:5); run;
|
p和q的范围不一定要0:5,可以根据之前的情况来判断。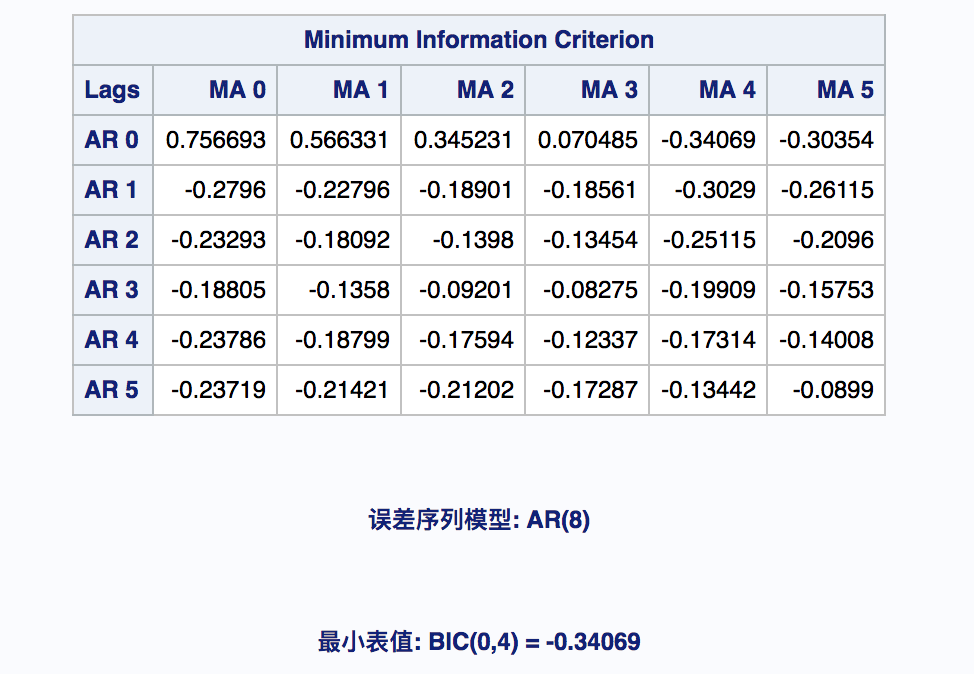
判断的标准如下

模型确定
其中因为ARMA(p,q)的取名,所以p是AR,q是MA。
可以加上noint以取消常数项的影响。
预测和绘图
1 2 3 4 5 6 7 8 9
| forecast lead=5 id=time out=results; run; proc gplot data=results; plot x*time=1 forecast*time=2 l95*time=3 u95*time=3/overlay; symbol1 c=black i=none v=star; symbol2 c=red i=join v=none; symbol3 c=green i=join v=none l=32; run;
|
lead的是预测长度。
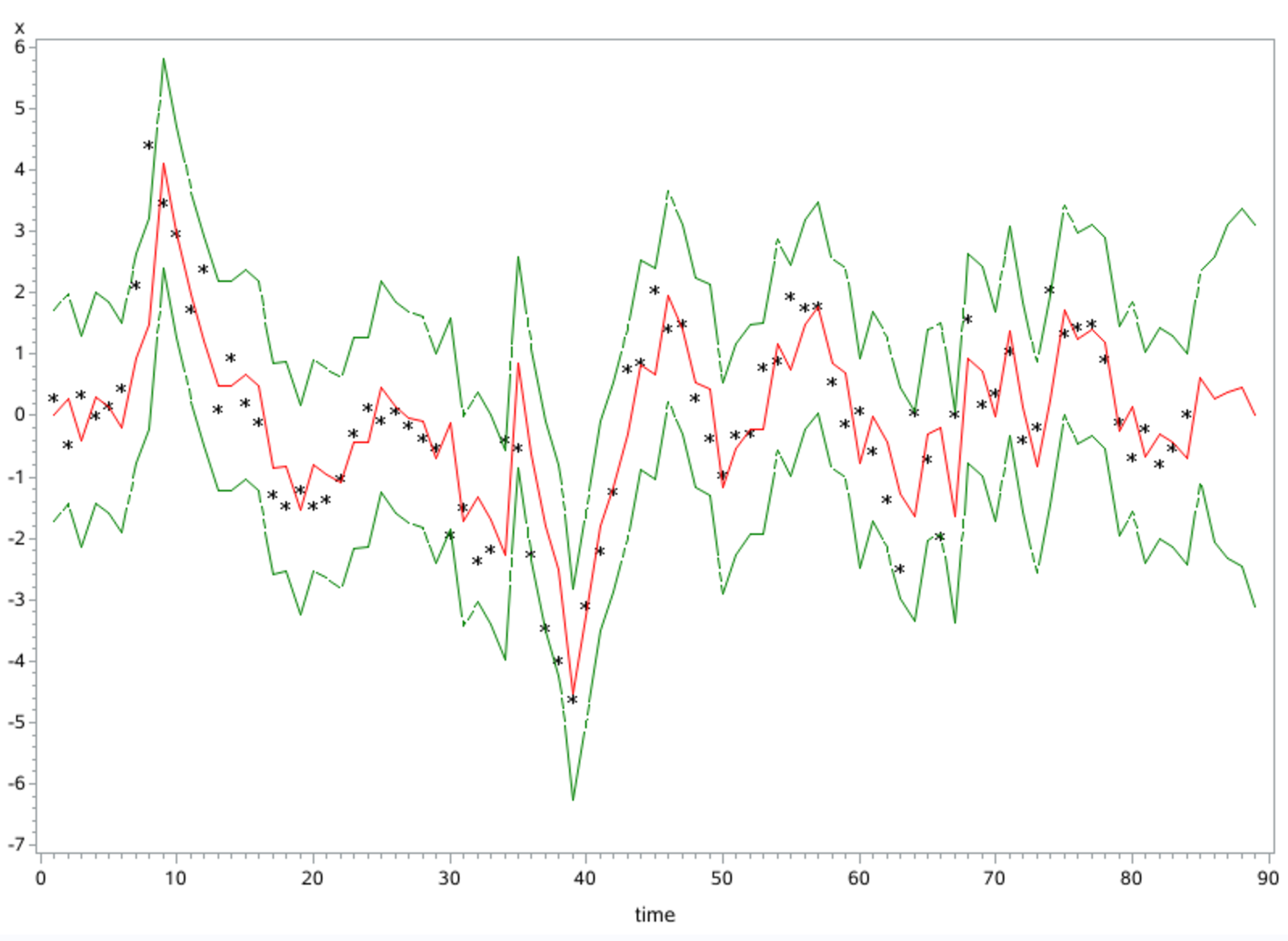
现阶段问题
1、非平稳序列如何平稳化?
2、图表中许多数据的意义不清楚。
的3.6上机指导。



